Third Grade Division Strategies

The introduction into the world of division from multiplication happens without pause. Within the same unit of study, students are introduced to both situations in an investigation. The only thing that changes between a multiplication and division situation is the unknown variable. In multiplication contexts, students are given the number of groups and the number of items within each group. They must find the total number of items in all.  On the other hand, in a division situation, students are given the total number of items and either the number of groups or the number of items in each group. They must find the missing piece of information.

Multiplication Situation

There are 5 bags of muffins. There are 4 muffins in each bag. How many muffins are there in all?

Number of Groups:  5

Number of Items in Each Group: 4

5x4=w

Division Situations

Situation 1:There are 20 muffins. There are 4 muffins in each bag. How many bags of muffins in all?

Situation 2:  There are 20 muffins in all. There are 5 bags of muffins. How many muffins are there in each bag?

Situation #1: 

Number of Groups:  ?

Number of Items in Each Group: 4

Total Number:  20

Equation:  20 ÷ 4 = b

Situation #2:

Number of Groups:  5

Number of Items in Each Group: ?

Total Number:  20

Equation:  20 ÷ 5 = m

Fact Family

Though the context changes, students often see division situations quite the same as the multiplication situation. They write the fact family to see if they know the answer quickly. Some students who think about fact families can solve a problem like this with mental math.

20 ÷ 4 = __

20 ÷ 5 = ___

5 x __ = 20

__ x 4 = 20

If they write the fact family but do not know the answer quickly, they can use repeated addition or skip counting to solve.

Repeated Addition

20 ÷ 4 = ___

4+4+4+4+4 = 20. There are 5 groups of 4 in 20.

20 ÷ 5 = ___

5+5+5+5 = 20. There are 4 groups of 5 in 20.

Skip Counting

20 ÷ 4 = ___

4, 8, 12, 16, 20  (The student skip counted 5 times.)

20 ÷ 5 = ___

5, 10, 15, 20 (The student skip counted 4 times.)

Ratio tables can also be used as a tool in division skip counting to organize a students’ thinking.

Successive Subtraction

Another early division strategy is successive subtraction.

20    ÷ 4 = ___

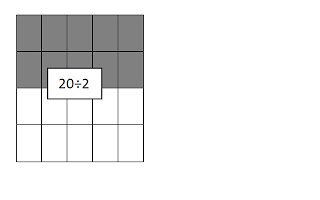
Array Model

Some students attack division using their knowledge of arrays.

20 ÷ 4 = ___

The student would build an array with 20 square units and then divide that area into groups of 4 square units. When finished dividing, they would count the number of groups they had created.

There are 5 groups of 4’s shaded.

This conceptual knowledge helps students build not only algebraic thinking, but fractions, too. In 4^th grade, students study dividing brownies into fractional parts.  

Multiplication Clusters

20 ÷ 4 = __

If students don't know how many fours are in 10, they can work with familiar fours. The student, in this example may know that 2 groups of 4 is 8 and 3 groups of 4 is 12, therefore 5 groups of 4 is 20.

(2 x 4) + (3 x 4)  = 20      

Division Clusters

20 ÷ 4 = ___

20 ÷ 4 can be thought of easily as 20 ÷ 2 =  10 and then 10 ÷ 2 =  5.

This, by no means is an exhaustive list, it simply highlights for you the division strategies which were covered through Closing Session in our third grade classroom during a week and a half of division work. The strategies are meant to build conceptual knowledge. Students are expected by the end of fourth grade to master the traditional algorithm in multiplication and division.

Multiplication Strategies

Young mathematicians’ first formal introduction to multiplication and division happens in 3rd Grade.

In our unit, Equal Groups, situations are presented in context. The situation usually requires students to identify the number of groups and the number of items within each group.

There are 5 tricycles. Each tricycle has three wheels. How many wheels are there in all?

Or, the situation may read,

Tricycles have three wheels. There are 5 tricycles. How many wheels are there in all?

Number of Groups: 5
Number of Items in Each Group: 3

Students are taught to represent the problem with both an addition equation and a multiplication equation to illustrate the connection, and use a variable for the missing piece of information.

Addition equation: 3+3+3+3+3=w
Multiplication equation: 5x3=w (read 5 groups of 3)

Students generally begin solving the multiplication situations with their prior knowledge of repeated addition.

Repeated Addition: 3+3+3=9 and 3+3=6, so 9+6=15.

Then, some students move into skip counting if they can easily skip count by that number. If the situation allows counting skip counting by 2’s, 5’s, and 10’s, students will almost always start with this strategy. If however, the situation has them skip counting by 8’s, then we’ll teach students to use 10 as their anchor. Skip count by 10 and go back 2.

Skip Counting: 3,6,9,12,15.

One tool that we teach students to use to organize their thinking when skip counting is a ratio table. Ratio tables help students keep track of the number of groups as they skip count.

During the unit, students are introduced to multiplication situations using arrays, too. An array is a rectangular arrangement with rows and columns.

To create a common language with our students, we have them give us the dimensions of the row first and then the column. The array above would be a 5x3.

There are many ways to solve the array. One of the things students do is skip count the array.
They can skip count the array be either the rows or columns.

Students naturally begin to see and explore the commutative property of multiplication. Though the situation is 5x3, they realize they can applying their number knowledge properties, and solve 3x5 instead (5,10,15 or 5+5+5=15).

Students’ next level of understanding develops when they recognize that they can decompose an array into smaller arrays to help them solve problems.

In this situation, if a student didn’t know the product of 5x3 quickly, they could decompose the array into (5x2) + (5x1) = 15.

This understanding is extremely important as students move into problems that are more difficult when they begin multiplication like 6x8. When in the early stages of developing automaticity, they may not know 6x8, but if they know (3x8), they can solve 2(3x8), or, if they know 6x4, they can solve 2(6x4).

Students’ ability to think flexibly with decomposing arrays in multiple ways, builds a strong foundation for fluency in multiplication. The skill allows students to attack any multiplication equation for which they don’t automatically have a product, and leads into being able to solve more difficult equations like 14 x 12.

After the unit, Equal Groups, students have a solid conceptual foundation and can think about multiplication flexibly. But, if we stop there, they may never become fully fluent. We continue to practice fact fluency with our combination club flash cards, by playing multiplication bingo, doing fluency clicker reviews, and doing a timed fluency snapshot several times a week. The fluency snapshots are presented by similar facts. (5’s and 10’s together) (2’s and 4’s and 8’s together) (3’s, 6’s, 9’s, 12’s together) (7’s) and (11’s). Presentation with similar facts promotes the conceptual understanding we build throughout this unit.

Our goal is for every student to leave third grade knowing each of their multiplication facts within three seconds. This foundational knowledge creates automaticity and will help them be successful in fourth grade as they embark on more complex multiplication problems like 49 x 58.

Dork in Disguise

Hey, Abigale here. I’m going to tell you about a GREAT story called Dork in Disguise!!! It’s about a kid named Jerry Flack and last year he was a dork. But this year he’s going to change. This year Jerry is going to become cool. He gets two girls attracted to him. One (the most popular girl in school) named Cinnamon. And two (the biggest brain in school) named Brenda. Which one will he choose? You’ll have to read the book to find out!!!
I Hope You Like The Book!!!
P.S. you can find it in the funny/humorous basket.

Ramona, Here We Come!

On Monday January 30th, we will be going to the Florida Theater to see a play based on the Ramona book series. All field trip money is due Friday, January 27th. The price for students is $10. The price for chaperones is $7.50. We are so excited for this special opportunity.